An Introduction to Formal Verification Techniques and Tools
Formal verification is the systematic process of validating the correctness of a system against certain rigorous formal criteria. In this post, we analyze different techniques and tools.
1. What is Formal Verification
Formal verification is the systematic process of validating the correctness of a system against certain rigorous formal criteria. It relies on constructing a mathematical model to represent the system and its desirable properties, and then uses logic and formal methods to demonstrate that the model complies with those properties under all possible operating conditions.
In contrast to conventional testing techniques that depend on examination and experimentation with specific instances, formal verification is oriented towards universality and conceptualization, asserting the validity of a program's properties for a complete range of states and possible inputs.
Using formal methods, the specifications and expected behaviors of a system are transformed into logical propositions and equations that are subject to rigorous verification or refutation, much like how in mathematics, a proposition like "a + b - b = a" remains invariably true for any set of integers.
2. Formal Verification Techniques
In this post, we will focus on symbolic execution, as it has more extensive development.
Symbolic Execution
Definition:
Symbolic execution is an advanced technique of formal verification that involves executing programs with symbolic variables instead of real values. This technique enables exhaustive analysis of a program's execution paths, effectively exploring all possible paths the program can take.
The result is a mathematical representation of the conditions and execution paths that can be used to test the program's correctness against a given specification or to discover conditions under which errors could occur.
Example:
Consider a simple function that calculates the maximum of two numbers, max(int a, int b). When applying symbolic execution, instead of executing the function with specific numbers (like max(2, 3)), the function is executed with symbolic values A and B.
This allows for the analysis of all possible conditions (A > B, A < B, A = B) to verify the correctness of the function in all possible cases.
Abstract Interpretation
Definition:
Abstract interpretation is a static analysis technique that provides a safe approximation of a program's behavior by abstracting certain details of the program's state to reduce complexity.
Example:
Imagine a loop that counts from 0 to n. Abstract interpretation could simplify the analysis by not considering each individual count value but abstracting the state to "counting" or "finished counting."
This way, properties such as loop termination can be verified without analyzing each individual iteration.
Model Checking
Definition:
Model checking is an automatic verification method that explores the state space of a system model to check if it satisfies specific logical properties.
Example:
Think of a traffic light system at an intersection. Using model checking, you could automatically verify if the traffic system model maintains the property of never having conflicting green lights (such as having green lights in two perpendicular directions at the same time), regardless of the order or timing of the lights.
Bytecode Verification
Definition:
Bytecode verification is a formal verification method that analyzes the bytecode of a program, which is the low-level representation to which the source code has been compiled.
This technique is crucial for validating program security and correct execution.
Example:
Suppose there is a smart contract managing an investment fund. During bytecode verification, the compiled code is analyzed to confirm that there are no possibilities for funds to be locked or sent to unauthorized addresses.
For example, it verifies that the bytecode ensures only the contract owner can withdraw funds, and only under the previously agreed-upon conditions in the contract.
3. Formal Verification Tools
There are many formal verification tools, but we will focus on analyzing them one by one in detail:
Halmos
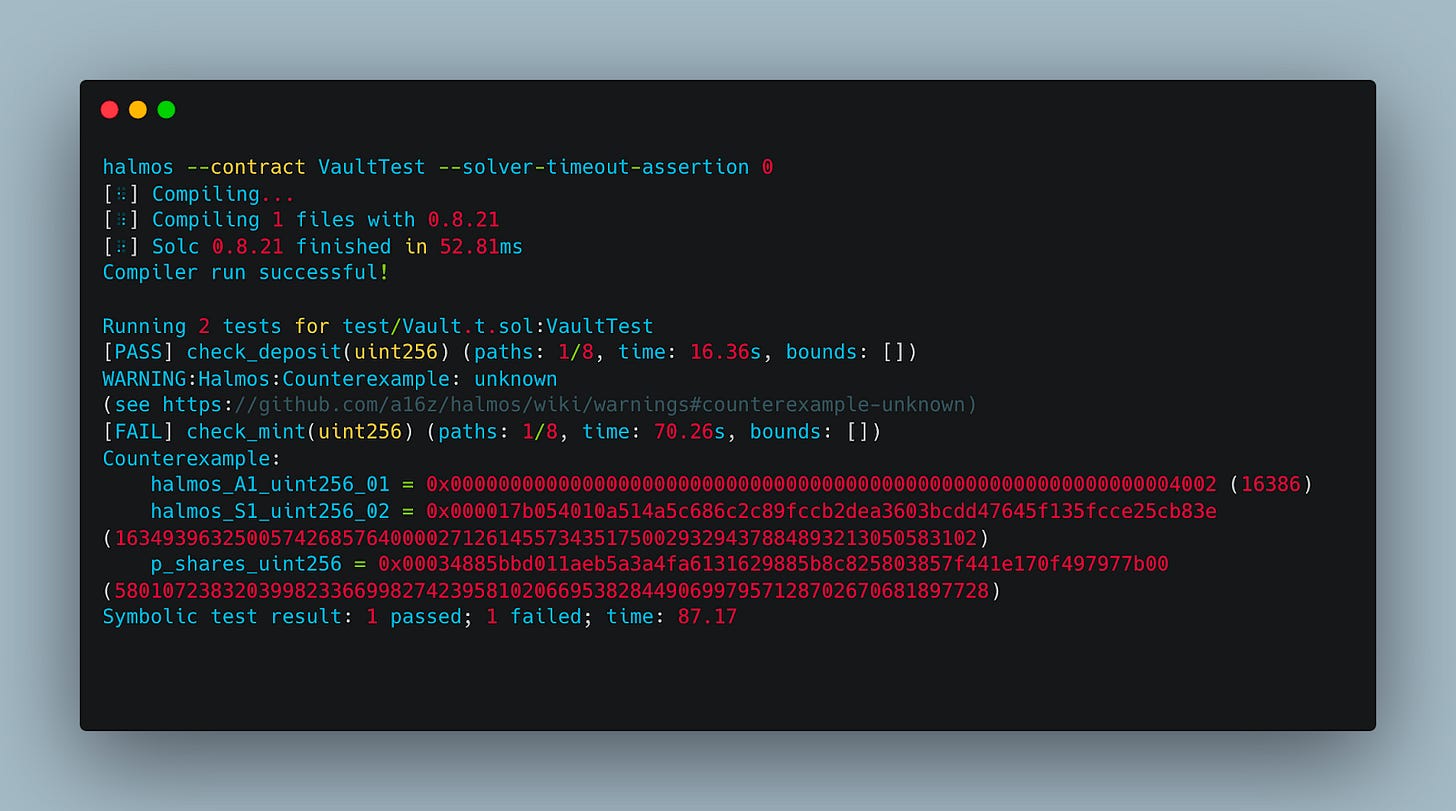
Halmos is an open-source formal verification tool that allows developers to reuse the same properties written for unit tests in formal specifications through symbolic testing.
A symbolic bounded model checker designed for symbolic testing of Ethereum smart contract bytecode. Halmos was developed by a16z.
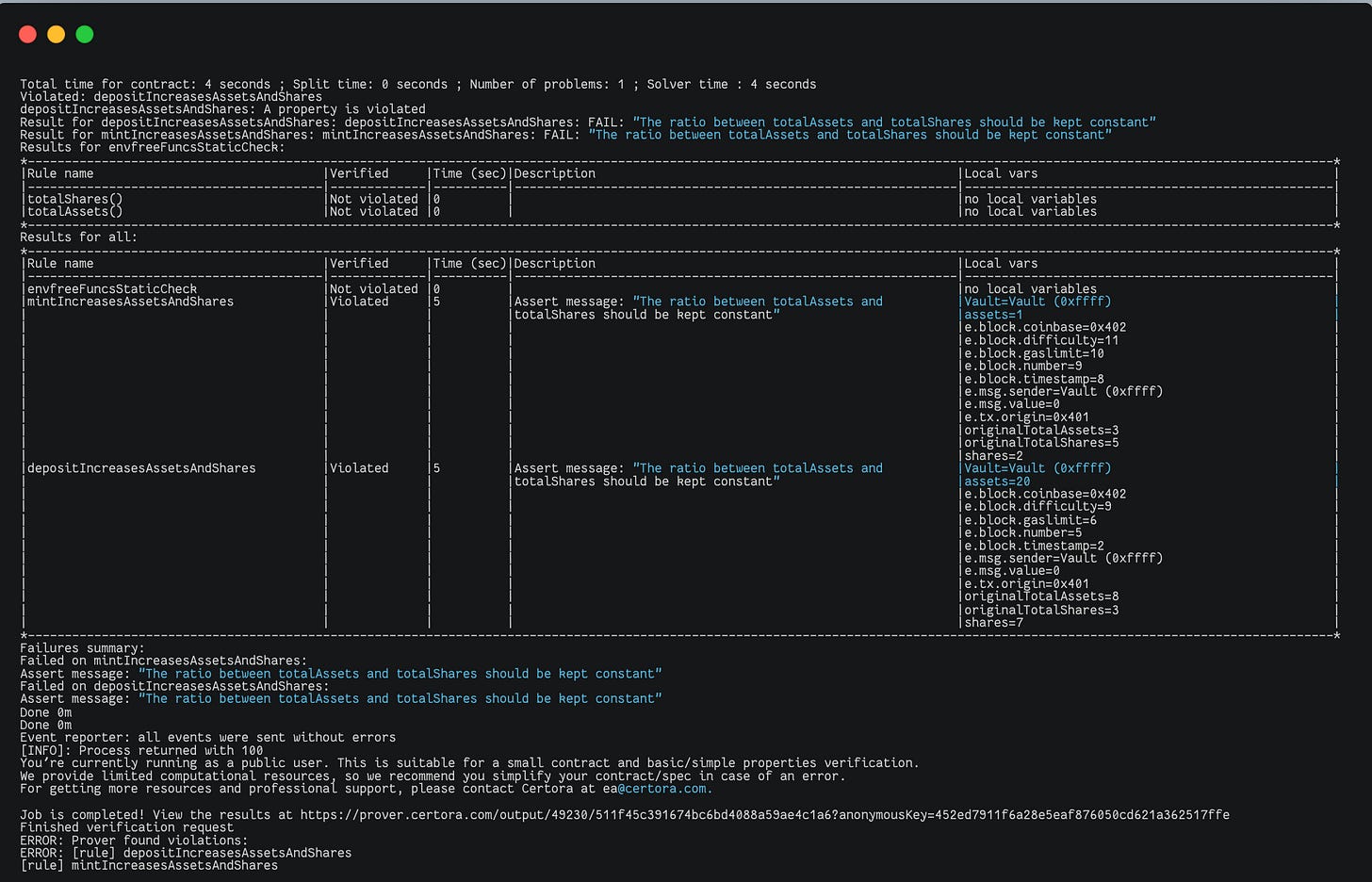
Certora
The Certora Prover is based on well-studied techniques from the formal verification community. Specifications define a set of rules that call into the contract under analysis and make various assertions about its behavior.
Together with the contract under analysis, these rules are compiled into a logical formula called a verification condition, which is then proved or disproved by an SMT solver. If the rule is disproved, the solver also provides a concrete test case demonstrating the violation.
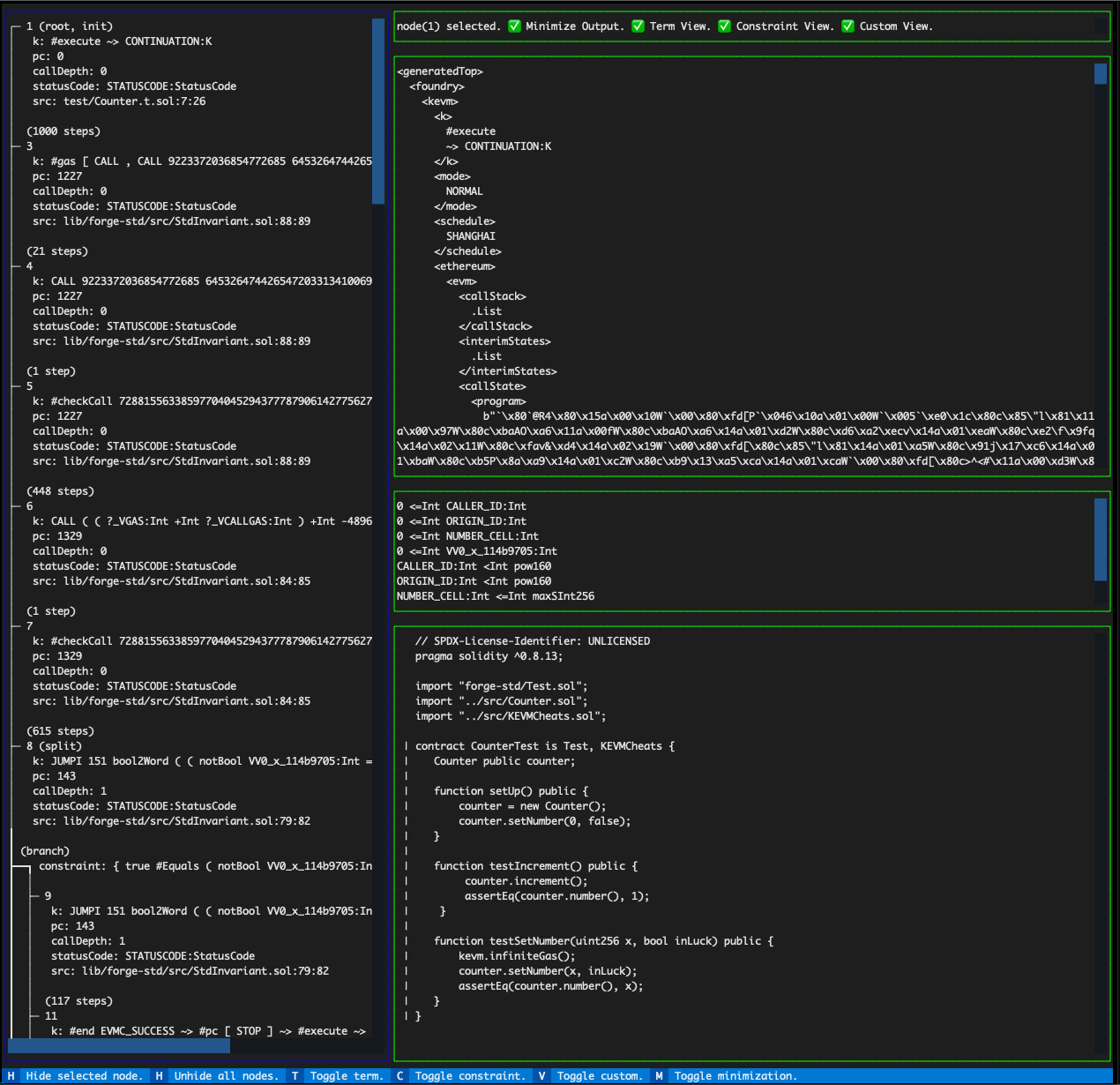
KEVM (Kontrol)
In this case, we are going to talk about Kontrol, which combines KEVM and Foundry. It grants developers the ability to perform formal verification without learning a new language or tool.
KEVM embodies a formal representation of the Ethereum Virtual Machine (EVM), established using the K Framework. This model serves various purposes, including the ability to carry out symbolic execution of smart contracts bytecode.
KEVM enables symbolic execution of Foundry tests and offers robust support for a wide array of Foundry cheatcodes. Furthermore, it introduces several supplementary cheatcodes.
It builds upon K, which is a versatile framework for crafting formal semantics and conducting verification, extending its capabilities beyond just the EVM.
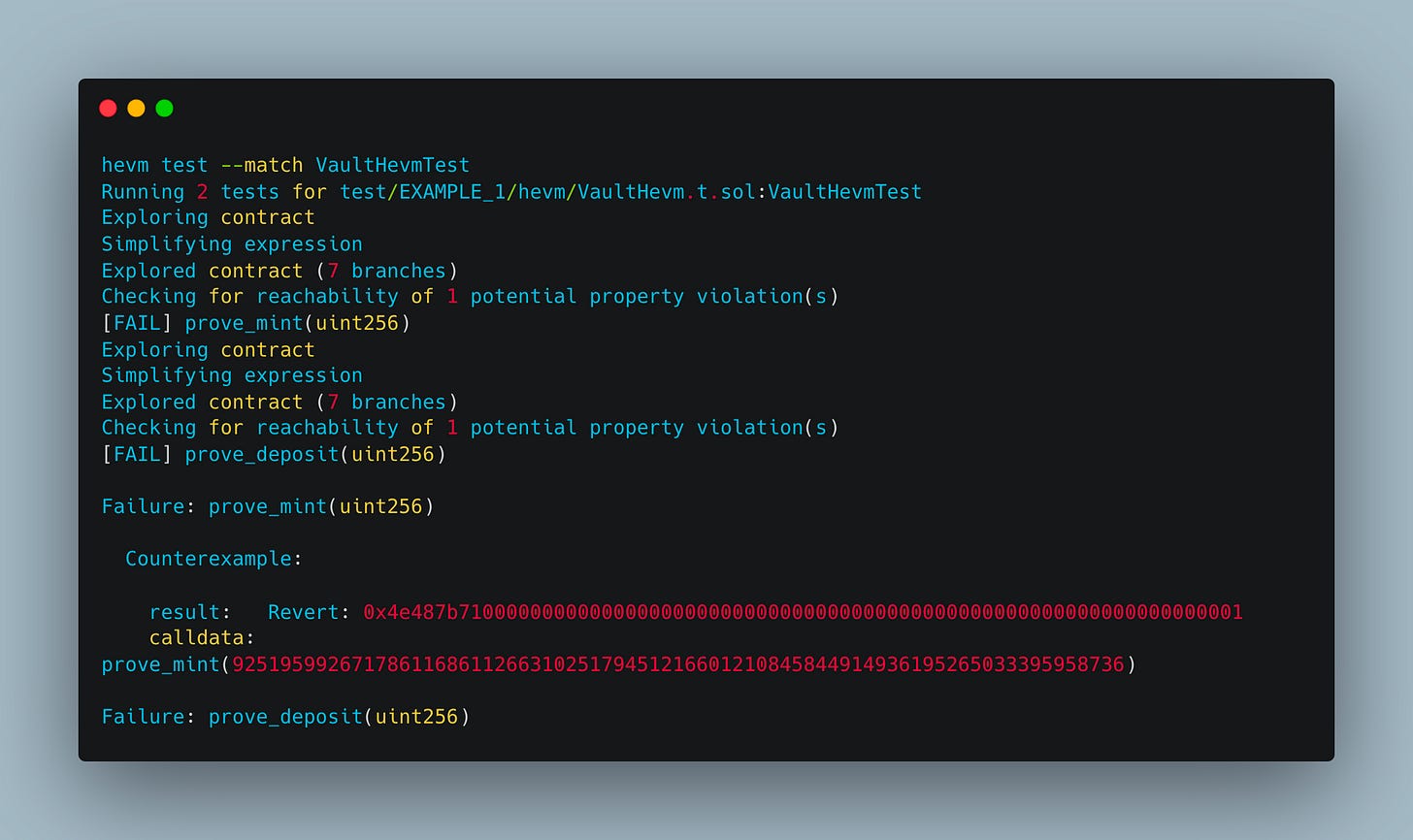
hevm
The hevm project is an implementation of the Ethereum virtual machine (EVM) made specifically for symbolic execution, unit testing, and debugging of smart contracts.
The hevm command line program can symbolically execute smart contracts, run unit tests, interactively debug contracts while showing the Solidity source, or run arbitrary EVM code.
Computations can be performed using a local state set up in a dapp testing harness or fetched on demand from live networks using RPC calls.
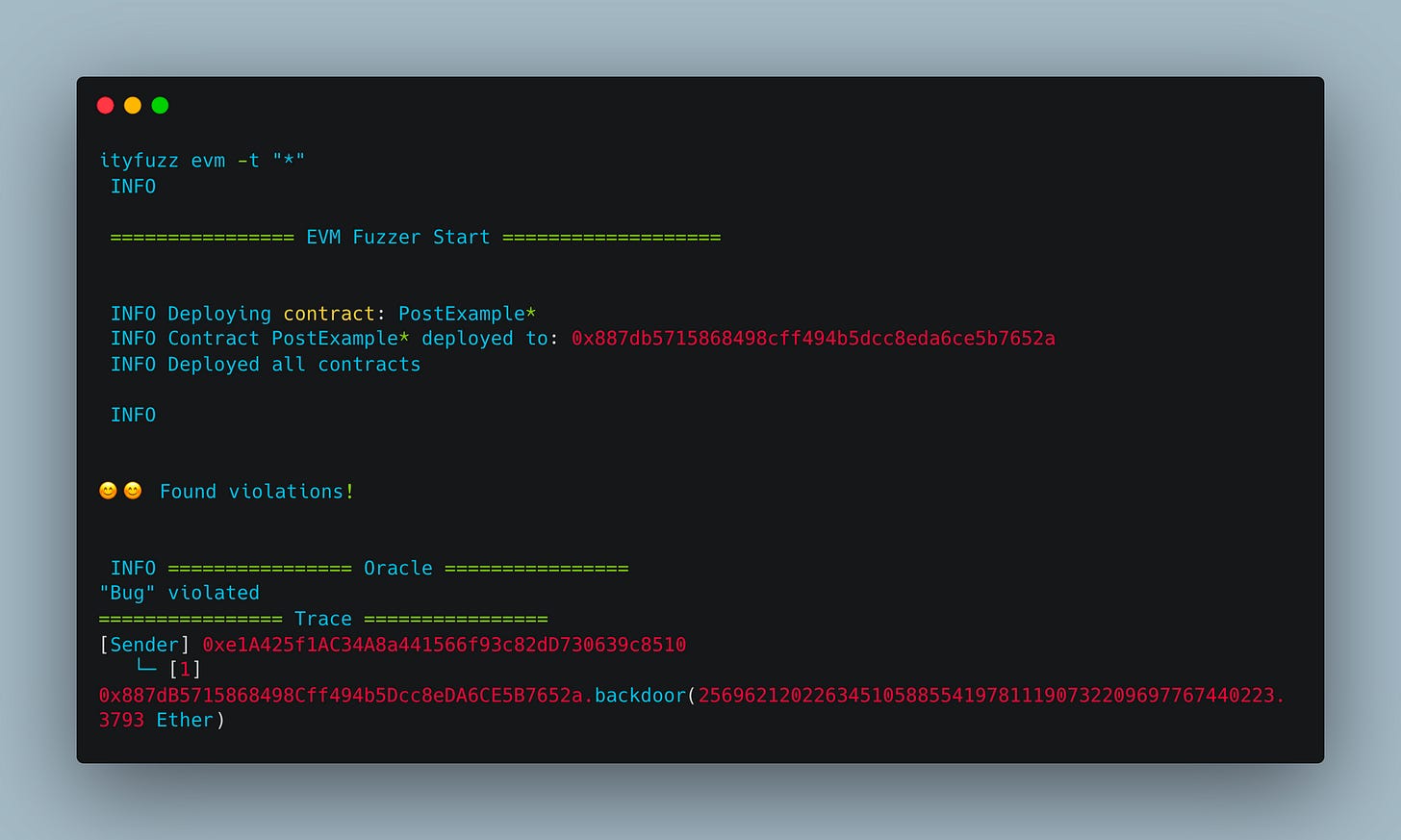
Ityfuzz
ItyFuzz is a smart contract hybrid fuzzer that combines symbolic execution and fuzzing to find bugs in smart contracts.
Technically, it leverages formal verification (concolic execution) assisted fuzzing algorithms guided by dataflow patterns and comparisons. ItyFuzz can handle DeFi with complex states and interactions and has been used to find many bugs in real-world smart contracts.
Conclusion
In this article, we explored the landscape of formal verification, a powerful tool for ensuring the reliability and security of software systems. We delved into various techniques such as symbolic execution, abstract interpretation, model checking, and bytecode verification. In future posts, we will help developers, researchers, and stakeholders better understand these tools and techniques by applying them to practical examples and analyzing their effectiveness in real-world scenarios.
Was it useful? Help us to improve!
With your feedback, we can improve the letter. Click on a link to vote: